Небесна сфера#
Поняття небесної сфери#
Небесна сфера - це уявна сфера довільного радіуса із центром у довільній точці спостереження, на яку спроектовані небесні світила. Розташування небесних тіл зображають у такому вигляді, як їх видно з центру небесної сфери у певний момент часу.
Небесна сфера виникла з практичної потреби опису положення зір у космічному просторі. Незважаючи на те, що зорі надзвичайно віддалені від Землі, і при спостереженні навіть через телескоп неможливо визначити, яка з них знаходиться далі, а яка ближче, нам здається, що всі небесні світила розташовані на однаковій відстані - на поверхні велетенської сфери, в центрі якої знаходиться спостерігач.
Залежно від розв'язуваної задачі, центр небесної сфери може бути розташований:
у місці на поверхні Землі, де перебуває спостерігач (топоцентрична небесна сфера),
у центрі Землі (геоцентрична небесна сфера),
у центрі тієї або іншої планети (планетоцентрична небесна сфера),
у центрі Сонця (геліоцентрична небесна сфера),
у будь-якій іншій точці простору, де перебуває спостерігач (реальний чи гіпотетичний).
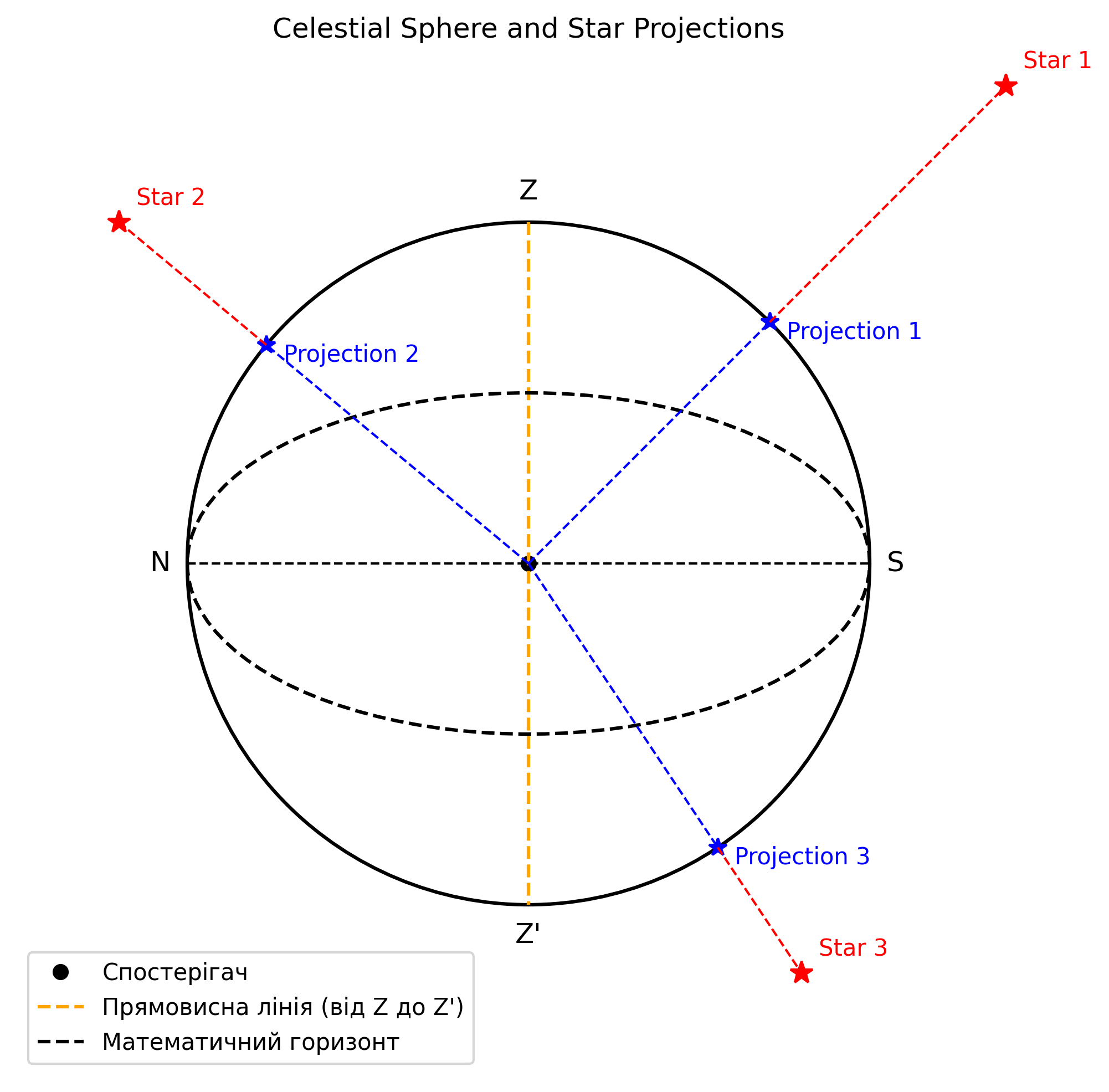
Image: Ілюстрація небесної сфери. На рисунку зображено три зірки, які перебувають на різній відстані від спостерігача, а також їх проекції на небесну сферу.
Елементи небесної сфери#
Для орієнтування на небесній сфері використовують систему координат та опорні точки (див. рисунки нижче). Ось основні з них:
Прямовисна лінія - це вертикальна лінія, що проходить через центр небесної сфери. Її напрямок визначається напрямком сили тяжіння. Верхня точка перетину цієї лінії з небесною сферою називається зенітом \(Z\), а нижня - надиром \(Z'\).
Площиною математичного (справжного) горизонту - площина, що перпендикулярна до прямовисної лінії. Математичний горизонт - велике коло небесної сфери, площина якого перпендикулярна до прямовисної лінії (тобто це коло, що утворюється в результаті перетину небесної сфери та площини математичного горизонту).
Коло висоти (або вертикальне коло) (\(ZMZ'\)) - це велике коло небесної сфери, що проходить через зеніт \(Z\), світило \(M\) і надир \(Z'\).
Вісь світу (\(P_NP_S\)) - це пряма, що проходить через центр небесної сфери паралельно осі обертання Землі. Точки перетину осі світу з небесною сферою називаються полюсами світу - Північним полюсом світу (\(P_N\)) та Південним полюсом світу (\(P_S\)).
Небесний екватор - це велике коло небесної сфери, перпендикулярне до осі світу. Він ділить небесну сферу на Північну півкулю з вершиною в Північному полюсі світу та Південну півкулю з вершиною в Південному полюсі світу.
Коло схилень світила (\(P_NMP_S\)) - це велике коло небесної сфери, що проходить через полюси світу \(P_N\) та \(P_S\) та через саме світило \(M\).
Небесний меридіан - велике коло небесної сфери, яке проходить через точки зеніта \(Z\), надира \(Z'\) та полюси світу \(P_N\) та \(P_S\). Небесний меридіан перетинається з математичним горизонтом у двох діаметрально протилежних точках. Точка перетину математичного горизонту й небесного меридіана, найближча до Північного полюса світу \(P_S\), називається точкою півночі \(N\). Точка перетину математичного горизонту й небесного меридіана, найближча до Південного полюса світу \(P_S\), називається точкою півдня \(S\). Пряма, що поєднує точки півночі й півдня, називається полуденною лінією (\(NS\)). Вона лежить на площині математичного горизонту.
Математичний горизонт з небесним екватором також перетинаються у двох діаметрально протилежних точках — точці сходу (\(E\)) та точці заходу (\(W\)). Якщо спостерігач стоїть в центрі небесної сфери обличчям до точки півночі, праворуч від нього буде розташована точка сходу, а ліворуч — точка заходу.
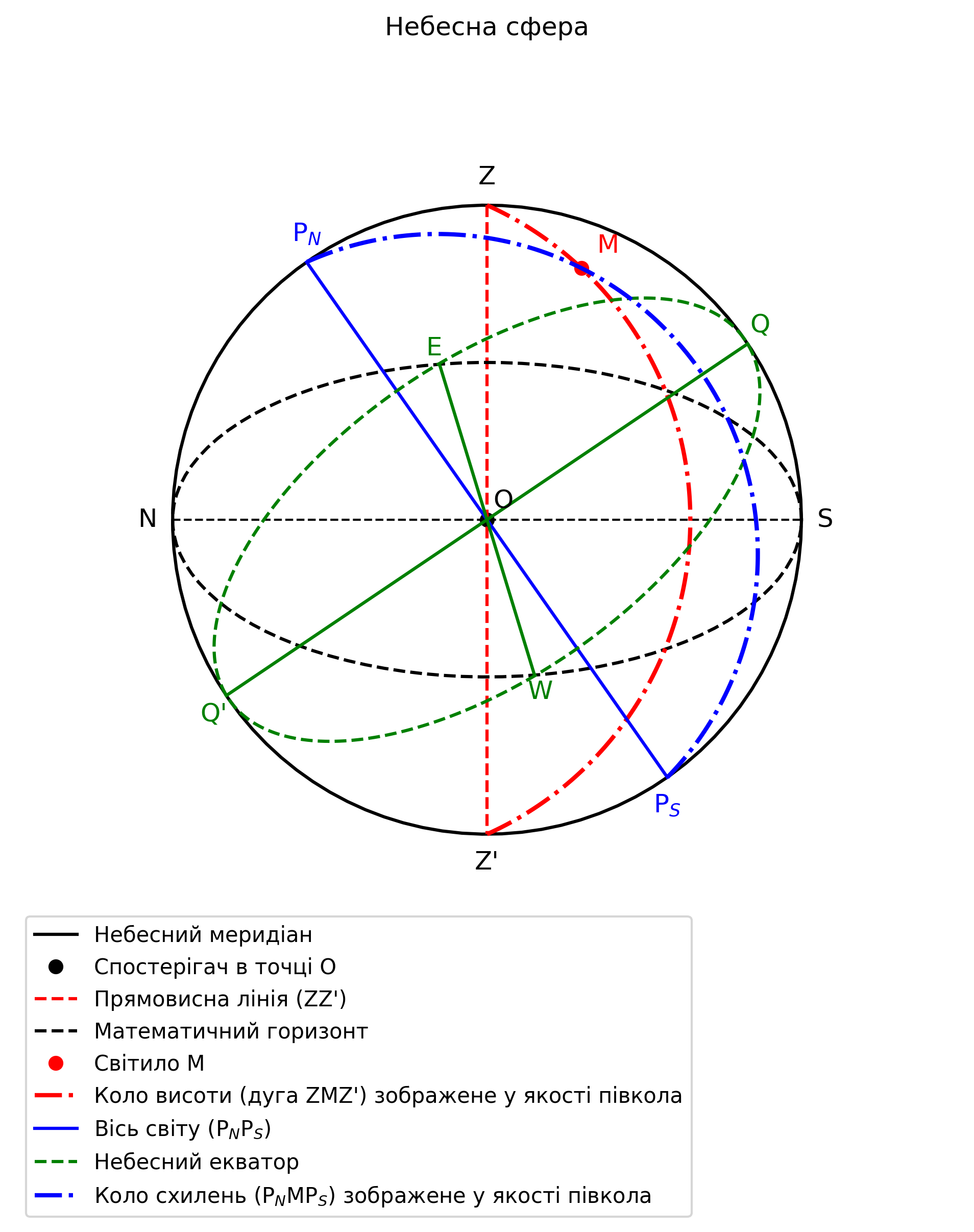
Image: Небесна сфера з основними лініями, площинами та точками (усі означення подані вище)
Примітка: код нижче генерує інтерактивну 3D модель небесної сфери, однак він занадто складний для новачків.
Show code cell source
import numpy as np
import plotly.graph_objs as go
from plotly.subplots import make_subplots
# ========================================================================
# Допоміжні функції
# ========================================================================
def normalize(v):
"""Нормує вектор v до довжини 1."""
return v / np.linalg.norm(v)
def param_sphere(num_phi=30, num_theta=60):
"""
Повертає сітки (X, Y, Z) для відмалювання сфери радіуса 1.
phi – полярний кут від 0 до pi,
theta – азимутальний кут від 0 до 2*pi.
"""
phi = np.linspace(0, np.pi, num_phi)
theta = np.linspace(0, 2*np.pi, num_theta)
phi, theta = np.meshgrid(phi, theta)
X = np.sin(phi) * np.cos(theta)
Y = np.sin(phi) * np.sin(theta)
Z = np.cos(phi)
return X, Y, Z
def circle_on_sphere(normal, steps=100):
"""
Повертає координати (x, y, z) великого кола на сфері,
яке лежить у площині, перпендикулярній до normal, і проходить через (0,0,0).
(normal має бути нормований).
"""
# Знайдемо будь-які два взаємно перпендикулярні вектори u, v у площині кола
# (тобто вони перпендикулярні до normal).
# Найпростіше – взяти довільний вектор, перетнути з normal, і ще раз перетнути з normal.
# Але простіше зафіксувати "eZ = (0,0,1)", якщо воно не вироджене до normal.
# Якщо normal (майже) колінеарний до (0,0,1), то можна взяти іншу "базу".
# Тут для наочності зробимо універсальний підхід.
# Умовно візьмемо eX = (1,0,0) і eY = (0,1,0), eZ = (0,0,1)
# і дивитимемось, з яким вектором normal найменше колінеарна.
cand = [
np.array([1,0,0]),
np.array([0,1,0]),
np.array([0,0,1])
]
# Знайдемо вектор, який найменше паралельний до normal (через косинус кута)
dotvals = [abs(np.dot(normal, c)) for c in cand]
e = cand[np.argmin(dotvals)]
# Будуємо базис у площині
u = np.cross(normal, e)
u = normalize(u)
v = np.cross(normal, u)
v = normalize(v)
# Випараметризуємо коло: X(t) = u*cos(t) + v*sin(t)
t = np.linspace(0, 2*np.pi, steps)
circle_x = []
circle_y = []
circle_z = []
for ang in t:
point = np.cos(ang)*u + np.sin(ang)*v
circle_x.append(point[0])
circle_y.append(point[1])
circle_z.append(point[2])
return np.array(circle_x), np.array(circle_y), np.array(circle_z)
def circle_through_3pts(p1, p2, p3, steps=200):
"""
Для трьох точок на сфері (p1, p2, p3) будуємо коло (або "велике/мале коло"),
що проходить через ці три точки (якщо вони не колінеарні).
Повертає (x_arc, y_arc, z_arc) – дугу на сфері, яка іде від p1 до p3
через p2 (тобто та частина кола, де p2 "лежить між" p1 та p3").
Ідея аналогічна вашій arc_from_3pts, але тепер у 3D:
1) Знаходимо площину, що проходить через p1, p2, p3 (через 0,0,0, якщо вважаємо сферу у центрі).
– Оскільки O=(0,0,0) теж у центрі сфери, припустимо, що p1, p2, p3 лежать на сфері радіуса 1.
2) Визначаємо вектор normal = (p1 x p2) + (p2 x p3) + (p3 x p1) (або простіше: p1 x p2 + ...),
щоб отримати "напрям" площини, у якій лежить коло.
3) Параметризуємо коло (intersection plane & sphere).
4) Визначаємо дві можливі дуги (бо коло – повне). Вибираємо ту, де p2 лежить "посередині".
"""
# Перевіримо, чи не колінеарні (або майже) p1, p2, p3.
# Якщо площа трикутника дуже мала – повертаємо порожній результат.
# Площа ~ ||(p2 - p1) x (p3 - p1)|| / 2
area = np.linalg.norm(np.cross(p2 - p1, p3 - p1)) / 2
if area < 1e-12:
return np.array([]), np.array([]), np.array([])
# Нормальний вектор до площини, що проходить через p1,p2,p3
# (і через (0,0,0), якщо точки на сфері).
# Точніше, normal визначимо як cross(p1, p2) + cross(p2, p3) + cross(p3, p1)
# Це забезпечить орієнтацію, яка "захоплює" всі три точки. Але можна й простіше:
plane_normal = np.cross(p1, p2) + np.cross(p2, p3) + np.cross(p3, p1)
plane_normal = normalize(plane_normal)
# Повне коло у цій площині
cx, cy, cz = circle_on_sphere(plane_normal, steps=4*steps) # щоб арка була плавніша
# Тепер треба знайти, де на цьому колі лежать p1, p2, p3 (кути).
# У параметризації кола X(t)=u cos(t)+v sin(t) ми заздалегідь не зберігали t,
# тож зробимо простіше: знайдемо найближчі індекси до p1, p2, p3.
# Допоміжна функція для пошуку найближчої точки
def find_nearest_idx(xarr, yarr, zarr, p):
# мінімізуємо відстань ||(x_i,y_i,z_i) - p||
dist = (xarr - p[0])**2 + (yarr - p[1])**2 + (zarr - p[2])**2
return np.argmin(dist)
i1 = find_nearest_idx(cx, cy, cz, p1)
i2 = find_nearest_idx(cx, cy, cz, p2)
i3 = find_nearest_idx(cx, cy, cz, p3)
# Кожна пара (i1,i3) задає дві дуги: прямий обхід і зворотний.
# Подивимось, яка з них "містить" i2.
n = len(cx)
def arc_indices(i_start, i_end):
"""Повертає послідовність індексів від i_start до i_end (по модулю n)."""
if i_end >= i_start:
return np.arange(i_start, i_end+1)
else:
return np.concatenate([np.arange(i_start, n), np.arange(0, i_end+1)])
arc1 = arc_indices(i1, i3)
arc2 = arc_indices(i3, i1)
# Перевіряємо, де лежить i2
def in_arc(i2, arc):
return i2 in arc
if in_arc(i2, arc1):
arc_idx = arc1
else:
arc_idx = arc2
return cx[arc_idx], cy[arc_idx], cz[arc_idx]
# ========================================================================
# Основна побудова 3D
# ========================================================================
# Створюємо фігуру
fig = make_subplots(rows=1, cols=1,
specs=[[{'type':'scatter3d'}]],
subplot_titles=["Небесна сфера в 3D"])
# 1) Небесна сфера як поверхня
Xs, Ys, Zs = param_sphere()
sphere_surface = go.Surface(
x = Xs, y = Ys, z = Zs,
colorscale='Blues',
opacity=0.3,
showscale=False,
name='Celestial Sphere'
)
fig.add_trace(sphere_surface, row=1, col=1)
# 2) Точки та лінії
data_traces = []
# --- Спостерігач у центрі ---
O = np.array([0, 0, 0])
scatter_O = go.Scatter3d(
x=[O[0]], y=[O[1]], z=[O[2]],
mode='markers+text',
text=["O"],
textposition="middle left",
marker=dict(size=5, color="black"),
name="Спостерігач (O)"
)
data_traces.append(scatter_O)
# --- Z та Z' (вертикальна вісь) ---
Z = np.array([0,0,1])
Zp = np.array([0,0,-1])
scatter_ZZp = go.Scatter3d(
x=[0,0], y=[0,0], z=[1,-1],
mode='lines+markers+text',
text=["Z", "Z'"],
textposition=["bottom left","bottom center"],
line=dict(color='red', width=3),
marker=dict(size=4, color="red"),
name="Прямовисна лінія (ZZ')"
)
data_traces.append(scatter_ZZp)
# --- Кардинальні точки N, S, E, W на площині z=0 ---
N = np.array([1,0,0])
S = np.array([-1,0,0])
E = np.array([0,-1,0])
W = np.array([0,1,0])
scatter_cardinals = go.Scatter3d(
x=[N[0], S[0], E[0], W[0]],
y=[N[1], S[1], E[1], W[1]],
z=[N[2], S[2], E[2], W[2]],
mode='markers+text',
text=["N","S","E","W"],
textposition=["middle right","middle left","bottom center","bottom center"],
marker=dict(size=5, color="green"),
name="Точка півночі (N), півдня (S), сходу (E), заходу (W)"
)
data_traces.append(scatter_cardinals)
# --- Горизонт (коло z=0 на сфері) ---
theta = np.linspace(0, 2*np.pi, 200)
horiz_x = np.cos(theta)
horiz_y = np.sin(theta)
horiz_z = np.zeros_like(theta)
scatter_horizon = go.Scatter3d(
x=horiz_x, y=horiz_y, z=horiz_z,
mode='lines',
line=dict(color='black', dash='dash', width=2),
name="Математичний горизонт"
)
data_traces.append(scatter_horizon)
# --- Вісь світу P_N, P_S з нахилом alpha = 35° ---
alpha_deg = 35
alpha = np.radians(alpha_deg)
# Припустимо, що у "стандартному" положенні полюс був би (0,0,1).
# Тоді повернемо його навколо осі Y на кут alpha (змінюючи нахил у площині x-z).
Ry = np.array([
[ np.cos(alpha), 0, np.sin(alpha)],
[ 0, 1, 0 ],
[-np.sin(alpha), 0, np.cos(alpha)]
])
PN = Ry.dot(np.array([0,0,1])) # Північний полюс
PS = -PN # Південний полюс
scatter_axis = go.Scatter3d(
x=[PN[0], PS[0]], y=[PN[1], PS[1]], z=[PN[2], PS[2]],
mode='lines+markers+text',
text=["P<sub>N</sub>", "P<sub>S</sub>"],
textposition=["top center","bottom center"],
line=dict(color='blue', width=3),
marker=dict(size=4, color="blue"),
name="Вісь світу"
)
data_traces.append(scatter_axis)
# --- Небесний екватор (велике коло перпендикулярне осі P_NP_S) ---
pn_normal = normalize(PN) # це напрям осі
eq_x, eq_y, eq_z = circle_on_sphere(pn_normal) # коло, перпендикулярне PN
scatter_equator = go.Scatter3d(
x=eq_x, y=eq_y, z=eq_z,
mode='lines',
line=dict(color='green', dash='dash', width=3),
name="Небесний екватор"
)
data_traces.append(scatter_equator)
# --- Приклад розташування світила M на сфері ---
# Нехай спочатку в 2D ви мали M=(0.3,0.8). У 3D додамо невеликий z і нормуємо:
M_init = np.array([0.4, 0.7, 0.5])
M = normalize(M_init)
scatter_M = go.Scatter3d(
x=[M[0]], y=[M[1]], z=[M[2]],
mode='markers+text',
text=["M"],
textposition="top center",
marker=dict(size=5, color='red'),
name="Світило (M)"
)
data_traces.append(scatter_M)
# --- "Вертикаль" (коло, що проходить через Z, M, Z') ---
v_x, v_y, v_z = circle_through_3pts(Z, M, Zp)
if len(v_x) > 0:
scatter_vertical = go.Scatter3d(
x=v_x, y=v_y, z=v_z,
mode='lines',
line=dict(color='red', width=3, dash='dot'),
name="Коло висоти (вертикальне коло) (ZMZ')"
)
data_traces.append(scatter_vertical)
# --- Коло схилень (через P_N, M, P_S) ---
d_x, d_y, d_z = circle_through_3pts(PN, M, PS)
if len(d_x) > 0:
scatter_decl = go.Scatter3d(
x=d_x, y=d_y, z=d_z,
mode='lines',
line=dict(color='blue', width=3, dash='dot'),
name="Коло схилень (P<sub>N</sub>MP<sub>S</sub>)"
)
data_traces.append(scatter_decl)
# --- Небесний меридіан (через Z, Z' та полюси світу P_N, P_S)
# Обираємо Z та P_N для визначення площини меридіану.
merid_plane_normal = normalize(np.cross(Z, PN))
merid_x, merid_y, merid_z = circle_on_sphere(merid_plane_normal, steps=200)
scatter_meridian = go.Scatter3d(
x=merid_x, y=merid_y, z=merid_z,
mode='lines',
line=dict(color='black', width=3),
name="Небесний меридіан"
)
data_traces.append(scatter_meridian)
# Додаємо всі лінії/точки до фігури
for tr in data_traces:
fig.add_trace(tr, row=1, col=1)
# Налаштування 3D-сцени
fig.update_layout(
# title="Небесна сфера в 3D",
scene=dict(
xaxis=dict(
range=[-1.5, 1.5],
showgrid=False, zeroline=False, visible=False
),
yaxis=dict(
range=[-1.5, 1.5],
showgrid=False, zeroline=False, visible=False
),
zaxis=dict(
range=[-1.5, 1.5],
showgrid=False, zeroline=False, visible=False
),
aspectmode='cube',
camera=dict(
eye=dict(x=0.8, y=0.5, z=0.3)
),
),
showlegend=True,
autosize=True,
height=800,
legend=dict(
orientation="v", # Display legend items horizontally
yanchor="top", # Anchor the top of the legend at the y position
y=-0.1, # Position the legend below the plot (adjust as needed)
xanchor="center", # Center the legend horizontally
x=0.5 # Centered at 50% of the width
),
margin=dict(l=0, r=0)
)
fig.show()
Екліптика#
Видимий річний шлях Сонця по геоцентричній небесній сфері (центр небесної сфери знаходиться в центрі Землі, однак небесна сфера не обертається разом із Землею) серед зір називається екліптикою. Екліптика перетинає небесний екватор у точках весняного та осіннього рівнодення. Ці точки відповідають моментам, коли тривалість дня майже дорівнює тривалості ночі (близько 20 березня та 22 вересня відповідно, хоча з року в рік ці дні можуть змінюватись).
Площина екліптики перетинається з площиною небесного екватора під кутом близько ε = 23°26', що дорівнює близько 23.4°.
На екліптиці також виділяють точки, що віддалені від точок рівнодення на 90°:
Точка літнього сонцестояння
Точка зимового сонцестояння
Для спостерігача на Північному полюсі Сонце досягає найвищої позиції на небі раз на рік у червні. День, коли це відбувається, називається днем літнього сонцестояння. Аналогічно, для спостерігача на Південному полюсі Сонце досягає найвищої позиції в день зимового сонцестояння. Коли на одному полюсі настає літнє сонцестояння, на іншому це зимове сонцестояння.
Коротко про сузір'я#
Сузір'я – це ділянки небесної сфери, які були умовно поділені астрономами для зручності орієнтування та класифікації об’єктів на нічному небі. Історично люди з’єднували яскраві зорі у вигляді фігур, але в сучасній астрономії сузір'я визначають як встановлені області (88 офіційно визнаних Міжнародним астрономічним союзом). У менш формальному контексті термін уживається на позначення назви групи зір, взаємне розташування яких складає якусь фігуру чи контур.

