Математичний і пружинний маятники#
Коливання пружинного маятника#
Пружинний маятник представляє собою коливальну систему, в якій тіло з'єднане з пружиною та здійснює періодичні коливання.
Дослідимо горизонтальний пружинний маятник, що складається з візка масою \(m\), прикріпленого пружиною з жорсткістю \(k\) до вертикальної стіни. За умови, що тертя в системі настільки мале, що ним можна знехтувати, коливання відбуватимуться без затухання - їхня амплітуда залишатиметься незмінною з часом, а повна механічна енергія зберігатиметься. У процесі коливань спостерігається постійне взаємне перетворення потенціальної енергії деформованої пружини в кінетичну енергію руху візка і навпаки.
Рис. 1. Горизонтальний пружинний маятник. Пружина знаходиться в рівноважному стані (А), стиснутому стані (В) і розтягнутому стані (С).
Public Domain, Link. Wiki
1. Стан максимального відхилення від положення рівноваги
Коли візок відхилений на максимальну відстань \(x_{max}\) від положення рівноваги вправо, пружина розтягнута максимально. У цьому положенні діє найбільша сила пружності, спрямована до положення рівноваги (вліво): \(F_{пруж} = kx_{max}\)
Оскільки візок у цей момент нерухомий, його кінетична енергія дорівнює нулю: \(E_k = 0\). Потенціальна енергія пружини досягає максимального значення і становить: \(E_p = \frac{kx^2_{max}}{2}\)
2. Прискорений рух візка, швидкість руху збільшується
Якщо відпустити візок, він почне рухатися вліво під дією сили пружності. Оскільки вектор сили \(\vec{F}_{пруж}\) спрямований у напрямку руху візка, швидкість руху зростає. Одночасно з цим деформація пружини зменшується, що призводить до зменшення сили пружності, а отже, й до зменшення прискорення візка.
При цьому відбувається перетворення енергії: кінетична енергія візка збільшується: \(E_k = \frac{mv^2}{2}\), а потенціальна енергія деформованої пружини зменшується: \(E_p = \frac{kx^2}{2}\). Загальна енергія системи залишається сталою і дорівнює сумі \(E = E_k + E_p\).
3. Стан рівноваги
Через проміжок часу, рівний чверті періоду коливань \((t = T/4)\), візок досягає положення рівноваги. В цей момент сила пружності та прискорення дорівнюють нулю, а швидкість візка сягає свого максимального значення.
У положенні рівноваги потенціальна енергія дорівнює нулю: \(E_p = 0\), а кінетична енергія максимальна: \(E_k = \frac{mv^2_{max}}{2}\), що дорівнює повній енергії системи.
4. Сповільнений рух візка, швидкість руху зменшується
Проходячи положення рівноваги, візок продовжує рух вліво за інерцією. Пружина починає стискатися, виникає і збільшується сила пружності, що напрямлена проти руху візка, гальмуючи його.
У цій фазі кінетична енергія візка поступово зменшується: \(E_k = \frac{mv^2}{2}\), а потенціальна енергія стисненої пружини збільшується: \(E_p = \frac{kx^2}{2}\). Сума цих енергій залишається незмінною.
5. Стан максимального відхилення від положення рівноваги
Коли візок досягає крайнього лівого положення (точки максимального відхилення), він на мить зупиняється. Сила пружності в цей момент досягає максимального значення, але в протилежному напрямку порівняно з початковим положенням. Від початку руху минає половина періоду коливань \((t = T/2)\).
У цьому положенні візок не рухається, тому кінетична енергія дорівнює нулю: \(E_k = 0\). Потенціальна енергія стисненої пружини максимальна: \(E_p = \frac{kx^2_{max}}{2}\)
У другій половині періоду процес повторюється в зворотному напрямку: візок рухається вправо, проходить положення рівноваги в момент часу \(t = \frac{3T}{4}\) і досягає початкового положення максимального відхилення вправо при \(t = T\), завершуючи повний цикл коливання. Після цього процес повторюється.
Важливо зазначити! Протягом усього процесу коливання сила пружності завжди спрямована до положення рівноваги, протидіючи зміщенню візка від цього положення.
Таким чином, вільні коливання пружинного маятника виникають завдяки двом ключовим факторам:
наявність сили, яка завжди спрямована до положення рівноваги;
інертність тіла, що коливається, через яку воно не зупиняється в положенні рівноваги (коли результуюча сила стає нульовою), а продовжує рух за інерцією.
Як визначити період коливань пружинного маятника#
Для визначення періоду коливань пружинного маятника проаналізуємо рух візка на горизонтальній пружині з позиції другого закону Ньютона. Векторна форма другого закону Ньютона має вигляд: \(\vec{F}_{пруж} + m\vec{g} + \vec{N} = m\vec{a}\).
Оскільки сила тяжіння \(m\vec{g}\) і сила нормальної реакції опори \(\vec{N}\) взаємно компенсуються, то \(\vec{F}_{пруж} = m\vec{a}\). При проектуванні цього рівняння на горизонтальну вісь ОХ отримуємо \(\left(F_{пруж.x} = ma_x\right)\). Використовуючи закон Гука \(\left(F_{пруж.x} = -kx\right)\), приходимо до рівняння:
Це рівняння можна подати у формі
що є характерним для гармонічних коливань. Тут циклічна частота коливань визначається як:
Враховуючи зв'язок між періодом і циклічною частотою \(T = \frac{2\pi}{\omega}\), отримуємо формулу для розрахунку періоду коливань пружинного маятника:
Важливо! Період коливань пружинного маятника залежить тільки від маси тіла \(m\) та жорсткості пружини \(k\), і не залежить від амплітуди коливань або гравітаційних умов (на Землі, в космосі, на Місяці тощо). Цю властивість можна використати для визначення маси об'єктів у невагомості, коли звичайні ваги не функціонують: знаючи жорсткість пружини \(k\) і вимірявши період коливань \(T\), можна обчислити масу \(m\).

Рис. 2. Вертикальний пружинний маятник.
Посилання. Wiki
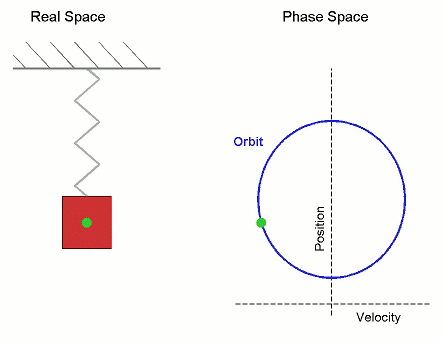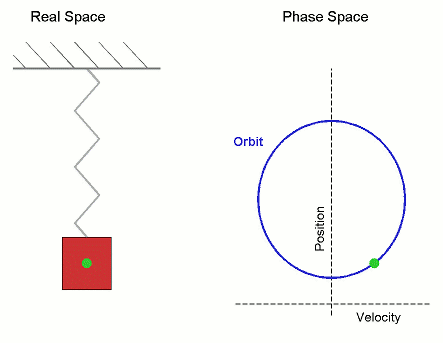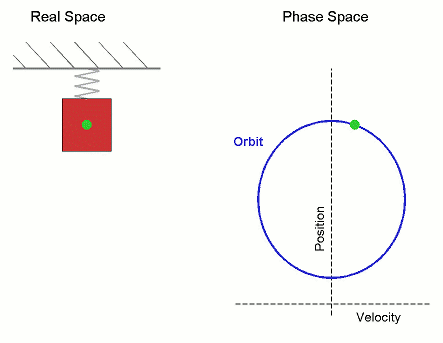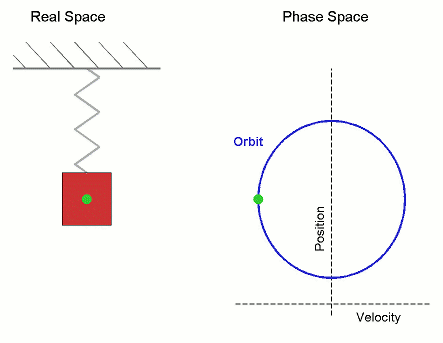
Рис. 3. Гармонічний рух, показаний як у реальному просторі, так і в фазовому просторі (орбіта періодична).
Public Domain, Link. Wiki
Що називають математичним маятником#
Тверде тіло, яке може коливатися відносно осі, що проходить через точку підвісу, називають фізичним маятником. Прикладом може бути підвішена на нитці іграшка в салоні автомобіля. При виведенні з рівноваги вона починає коливатися. Однак аналіз таких коливань є складним, оскільки на них впливають розміри та форма тіла, властивості нитки та інші фактори.
Для спрощення дослідження коливань використовують ідеалізовану модель - математичний маятник. Щоб створити таку модель, необхідно:
використати нитку, довжина якої значно перевищує розміри підвішеного тіла;
забезпечити, щоб маса нитки була набагато меншою за масу тіла, що дозволяє розглядати тіло як матеріальну точку;
нитка має бути нерозтяжною, щоб відстань від тіла до точки підвісу залишалася сталою.
Математичний маятник - це фізична модель, що складається з матеріальної точки, підвішеної на невагомій нерозтяжній нитці в полі сили тяжіння.
Коливання математичного маятника#
Якщо взяти невелику, але досить важку кульку і підвісити її на довгій тонкій нитці, то отримаємо систему, яку можна розглядати як математичний маятник. При відхиленні кульки від положення рівноваги та її відпусканні, під дією сили тяжіння та сили натягу нитки, вона почне коливатися.
За умови, що опір повітря незначний, а діями сили є консервативними, повна механічна енергія системи зберігатиметься. Під час коливань відбуватиметься взаємне перетворення потенціальної енергії піднятої кульки в кінетичну енергію її руху і навпаки.
Спостерігаючи за рухом такого маятника, можна аналізувати причини його руху та енергетичні перетворення, що відбуваються в різних фазах коливання.
Рис. 4. Математичний маятник (виконує гармонічний рух в умовах відсутності затухання і малої амплітуди).
By Krishnavedala - Own work, CC0, Link. Wiki
Як обчислити період коливань математичного маятника#
Математичний аналіз показує, що при малих кутах відхилення (приблизно 3–5°) математичний маятник здійснює гармонічні коливання. Це означає, що прискорення руху кульки пропорційне її зміщенню від положення рівноваги і спрямоване в протилежний бік: \(a_x = -\omega^2 x\).
Для математичного маятника циклічна частота визначається як
де \(g\) - прискорення вільного падіння, а \(l\) - довжина маятника.
Отже, період коливань математичного маятника обчислюється за формулою:
Ця формула була вперше виведена в XVII столітті нідерландським фізиком Крістіаном Гюйгенсом і відома як формула Гюйгенса.
Важливо відзначити, що період коливань математичного маятника не залежить від маси підвішеного тіла, а визначається лише довжиною нитки та прискоренням вільного падіння в місці розташування маятника. Ця властивість дозволяє використовувати математичний маятник для визначення прискорення вільного падіння: вимірявши довжину нитки і період коливань, можна обчислити значення \(g\) у даній місцевості.
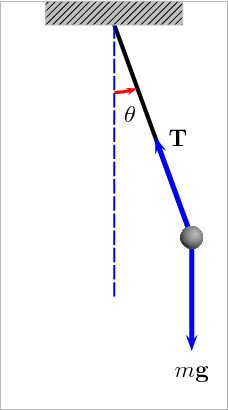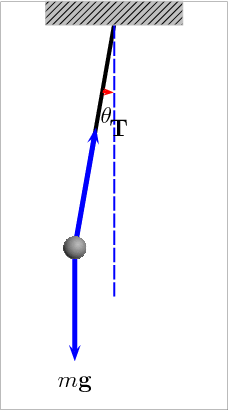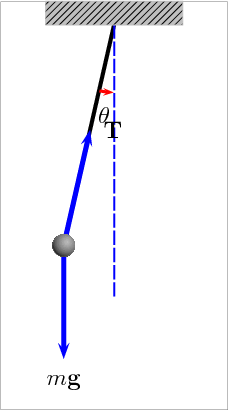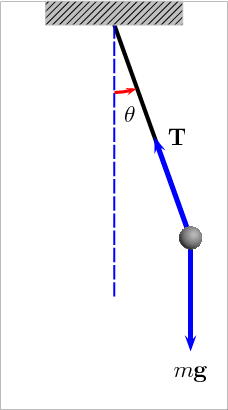
Рис. 5. Анімація математичного маятника, що демонструє сили, що діють на кульку: натяг T у стрижні та гравітаційна сила mg.
By Ruryk - Own work, CC BY-SA 3.0, Link. Wiki

Рис. 6. Анімація математичного маятника, що показує вектори швидкості та прискорення.
By Ruryk - Own work, CC BY-SA 3.0, Link. Wiki
Рис. 7. Діаграма сил для математичного маятника.
By Krishnavedala - Own work, CC BY-SA 3.0, Link. Wiki

Рис. 8. Тригонометрія математичного маятника.
CC BY-SA 4.0, Link. Wiki
Задача#
Тягар на пружині здійснює коливання за рівнянням: \(x = 20\cos(2\pi t)\) (см). Визначити повну механічну енергію системи, максимальну швидкість руху тягаря, а також кінетичну та потенціальну енергії через \(\frac{1}{6}\) с після початку коливань. Маса тягаря становить 1 кг. Систему вважати замкненою.
Вихідні дані:
\(x = 0.20\cos2\pi t\) (м)
\(t = \frac{1}{6}\) с
\(m = 1.0\) кг
Знайти: \(E\), \(v_{max}\), \(E_k\), \(E_p\)
Аналіз та розв'язання:
У замкненій системі виконується закон збереження повної механічної енергії:
\(E = \frac{kA^2}{2} = \frac{mv^2_{max}}{2} = E_k + E_p\).
Порівнюючи рівняння коливань у загальному вигляді \(x = A\cos\omega t\) з рівнянням у задачі \(x = 0.2\cos(2\pi t)\), знаходимо:
\(A = 0.2\) м – амплітуда коливань
\(\omega = 2\pi\) с\(^{-1}\) – циклічна частота
Із співвідношення \(\omega = \sqrt{\frac{k}{m}}\) визначаємо жорсткість пружини:
\(k = \omega^2m = 4\pi^2 \cdot 1 \approx 40\) Н/м
Повна механічна енергія системи:
\(E = \frac{kA^2}{2} = \frac{40 \cdot (0.2)^2}{2} = 0.8\) Дж
Максимальна швидкість руху тягаря:
\(v_{max} = A\omega = 0.2 \cdot 2\pi = 1.26\) м/с
Для визначення кінетичної та потенціальної енергій у момент часу \(t = \frac{1}{6}\) с знаходимо зміщення тягаря:
\(x = 0.2\cos\left(2\pi \cdot \frac{1}{6}\right) = 0.2\cos\frac{\pi}{3} = 0.2 \cdot 0.5 = 0.1\) м
Потенціальна енергія пружини в цей момент:
\(E_p = \frac{kx^2}{2} = \frac{40 \cdot (0.1)^2}{2} = 0.2\) Дж
Кінетична енергія:
\(E_k = E - E_p = 0.8 - 0.2 = 0.6\) Дж
Відповідь: \(E = 0.8\) Дж; \(v_{max} = 1.26\) м/с; \(E_k = 0.6\) Дж; \(E_p = 0.2\) Дж.

