Послідовне та паралельне з'єднання провідників#
Послідовне з'єднання провідників#
Послідовним називають з'єднання провідників, при якому вони розташовані один за одним без розгалужень. При такому з'єднанні електричний струм, проходячи через один провідник, обов'язково проходить і через усі інші.
Розглянемо ділянку кола, яка містить два послідовно з'єднані резистори (Рис. 2), і виведемо загальні співвідношення для будь-якої кількості послідовно з'єднаних провідників.
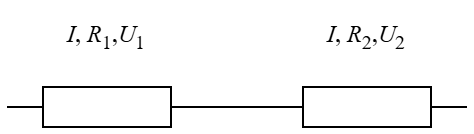
Рис. 2. Послідовне з'єднання провідників
При послідовному з'єднанні сила струму в усіх провідниках однакова і дорівнює загальній силі струму в ділянці кола.
Це пояснюється тим, що електричне коло з послідовним з'єднанням не містить розгалужень, тому заряд, який проходить через поперечний переріз будь-якого провідника за певний час \(t\), буде однаковим:
Ділячи обидві частини рівності на \(t\), отримуємо:
За означенням сили струму: \(\frac{q}{t} = I\). Отже:
\[I_1 = I_2 = I\]
Загальна напруга на послідовно з'єднаних провідниках дорівнює сумі напруг на цих провідниках. Коли заряд \(q\) переміщується під дією електричного поля, воно виконує роботу \(A_1\) в першому провіднику і \(A_2\) у другому. Оскільки для переміщення цього заряду через обидва провідники має бути виконана робота \(A = A_1 + A_2\), то, поділивши обидві частини рівності на заряд \(q\) і використовуючи означення напруги (\(U = \frac{A}{q}\)), маємо:
\[U = U_1 + U_2\]
Загальний опір послідовно з'єднаних провідників дорівнює сумі опорів цих провідників. Дійсно, якщо візьмемо до уваги попередньо отриманий результат \(U = U_1 + U_2\) і застосуємо до цієї формули закон Ома, то отримаємо:
Оскільки \(I_1 = I_2 = I\), отримуємо: \(IR = I R_1 + I R_2 = I(R_1 + R_2)\), звідки
\[R = R_1 + R_2\]
Отриманий результат можемо легко узагальнити на випадок \(n\) провідників, з'єднаних послідовно:
\[I_1 = I_2 = ... = I_n = I\]
\[U = U_1 + U_2 + ... + U_n\]
\[R = R_1 + R_2 + ... + R_n\]
Додаткові наслідки:
Загальний опір провідників, з'єднаних послідовно, завжди більший за опір кожного з цих провідників.
Загальний опір \(n\) послідовно з'єднаних провідників з однаковим опором \(R_0\) дорівнює \(R = nR_0\).
Паралельне з'єднання провідників#
З'єднання провідників називається паралельним, якщо для проходження струму існує два чи більше шляхів (гілок), і всі ці гілки мають одну пару спільних точок — вузлів (Рис. 3). У вузлах (вузлових точках) відбувається розгалуження кола (у кожному вузлі з'єднуються не менш ніж три провідники).
Розглянемо ділянку кола, яка містить два паралельно з'єднані резистори.
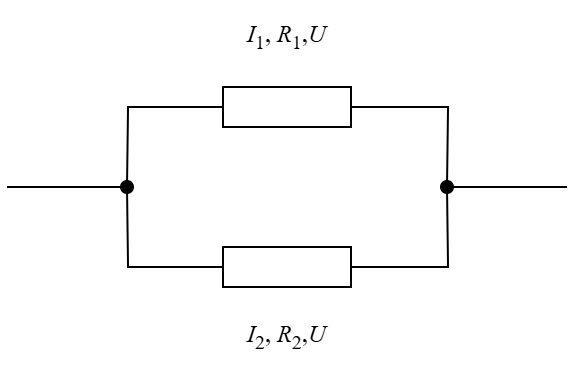
Рис. 3. Паралельне з'єднання провідників
При паралельному з'єднанні загальна сила струму в нерозгалуженій частині кола дорівнює сумі сил струмів у відгалуженнях (окремих гілках).
У вузловій точці струм розтікається по двох гілках. Заряд у вузловій точці не накопичується, тому заряд \(q\), який надійшов у вузол за певний час \(t\), дорівнює сумі зарядів, які вийшли з цього вузла за той самий час: \(q = q_1 + q_2\).
Поділивши обидві частини рівності на \(t\) і беручи до уваги, що \(\frac{q}{t} = I\), маємо:
\[I = \frac{q_1}{t} + \frac{q_2}{t} = I_1 + I_2\]
Загальна напруга на ділянці кола та напруга на кожному з паралельно з'єднаних провідників є однаковими. Якщо ділянка кола не містить джерел струму, то напруга на ділянці дорівнює різниці потенціалів на кінцях цієї ділянки. Таким чином, напруга усієї ділянки дорівнює \(U = \varphi_L - \varphi_R\), де \(\varphi_L\) та \(\varphi_R\) - потенціали у лівій вузловій точці та правій вузловій точці відповідно. Напруга для ділянки із опором \(R_1\) дорівнює \(U_1 = \varphi_L - \varphi_R\), а напруга для ділянки із опором \(R_2\) дорівнює \(U_2 = \varphi_L - \varphi_R\). Праві частини усіх цих виразів однакові, тому:
\[U = U_1 = U_2\]
Величина, обернена до загального опору розгалуженої ділянки кола, дорівнює сумі величин, кожна з яких обернена до опору відповідної гілки цього розгалуження. Доведемо це.
Оскільки \(I = I_1 + I_2\), то за законом Ома: \(\frac{U}{R} = \frac{U_1}{R_1} + \frac{U_2}{R_2}\). А оскільки \(U = U_1 = U_2\), то \(\frac{U}{R} = U(\frac{1}{R_1} + \frac{1}{R_2})\). Після скорочення на \(U\) отримуємо:
\[\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2}\]
Звідси, можемо отримати:
та
Додаткові наслідки:
Загальний опір паралельно з'єднаних провідників менший від опору кожного з цих провідників.
Загальний опір \(n\) паралельно з'єднаних провідників з однаковим опором \(R_0\) дорівнює \(R = \frac{R_0}{n}\).
Отриманий результат можемо легко узагальнити на випадок \(n\) провідників, з'єднаних паралельно:
\[I = I_1 + I_2 + ... + I_n\]
\[U = U_1 = U_2 = ... = U_n\]
\[\frac{1}{R} = \frac{1}{R_1} + \frac{1}{R_2} + ... + \frac{1}{R_n}\]

