Індуктивність та самоіндукція#
При зміні магнітного поля навколо провідника в ньому виникає вихрове електричне поле. Це відбувається незалежно від того, чим спричинена зміна магнітного поля - зовнішніми чинниками чи змінним струмом у самому провіднику. Важливо розуміти, що провідник не розрізняє джерело магнітного поля - власне воно чи зовнішнє. Розглянемо детальніше фізичні явища, які виникають коли провідник знаходиться у власному змінному магнітному полі.
Явище самоіндукції#
Для демонстрації цього явища створимо електричне коло з двома лампами. Характерна особливість такого досліду: при замиканні кола лампа 1 засвічується майже миттєво, тоді як лампа 2 вмикається з відчутною затримкою. Цікаво, що під час розмикання обидві лампи гаснуть одночасно.
Що відбувається при замиканні кола? Одразу після замикання сила струму в колі починає зростати. Всередині котушки формується змінне магнітне поле, магнітна індукція \(\vec{B}\) якого також збільшується. Це змінне магнітне поле генерує вихрове електричне поле \(\vec{E}\), яке відповідно до правила Ленца протидіє струму в котушці. Саме через цю протидію сила струму в котушці й у нижній лампі (див. Рис. 1) зростає не миттєво, а поступово. Хоча в провідниках, що підводять струм до верхньої лампи, теж виникає вихрове електричне поле, але створена ним ЕРС настільки мала, що практично не впливає на роботу схеми.
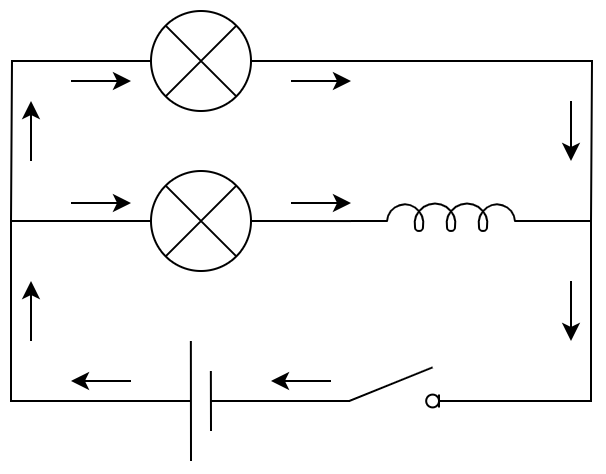
Рис. 1. Напрямок струму при замиканні кола.
А що відбувається при розмиканні кола? Відразу після розмикання сила струму в колі починає зменшуватись, відповідно зменшується й магнітна індукція \(\vec{B}\) поля, створеного цим струмом. Зміна магнітного поля породжує вихрове електричне поле \(\vec{E}\), яке за правилом Ленца підтримує струм у котушці. Хоча здавалося б, що нижня лампа повинна згаснути пізніше верхньої лампи (див. Рис. 2), вони вимикаються одночасно. Пояснюється це тим, що коло з двох ламп, котушки та резистора залишається замкненим. Котушка в цій ситуації діє як джерело струму: вихрове електричне поле в котушці підтримує струм у колі протягом деякого часу. При цьому струм через котушку й нижню лампу продовжує текти в тому ж напрямку, а у верхній лампі напрямок струму змінюється на протилежний.
Це явище утворення вихрового електричного поля в провіднику при протіканні змінного електричного струму називається явищем самоіндукції.
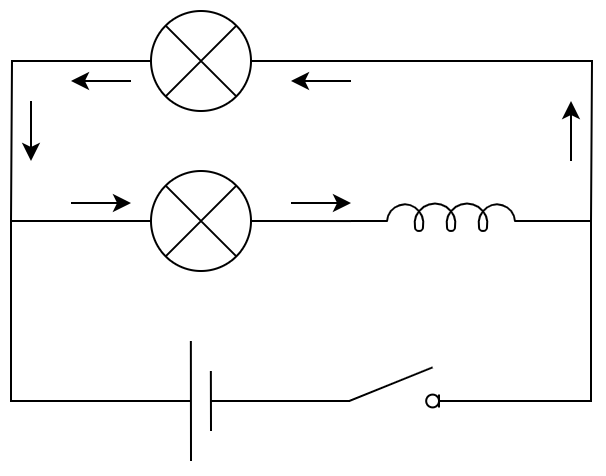
Рис. 2. Напрямок струму при розмиканні кола.
ЕРС самоіндукції. Індуктивність#
Електрорушійною силою самоіндукції \(\varepsilon_{is}\) називають ЕРС індукції, що виникає в провіднику через зміну його власного магнітного поля.
Згідно із законом Фарадея, ЕРС самоіндукції прямо пропорційна швидкості зміни магнітного потоку: \(\varepsilon_{is} = -\frac{\Delta \Phi}{\Delta t} = -\Phi'(t)\). Оскільки магнітний потік прямо пропорційний магнітній індукції магнітного поля струму \((\Phi \sim B)\), а магнітна індукція прямо пропорційна силі струму в провіднику \((B \sim I)\), можна стверджувати, що магнітний потік прямо пропорційний силі струму в провіднику: \(\Phi = LI\), де \(L\) - коефіцієнт пропорційності. Відповідно, зміна магнітного потоку пропорційна зміні сили струму: \(\Delta\Phi = L\Delta I\).
Таким чином, можемо сформулювати закон самоіндукції:
ЕРС самоіндукції прямо пропорційна швидкості зміни сили струму в провіднику:
\[ \varepsilon_{is} = -\frac{\Delta \Phi}{\Delta t} = -L\frac{\Delta I}{\Delta t} \]
або
\[ \varepsilon_{is} = -LI'(t)\]
Коефіцієнт пропорційності \(L\) називають індуктивністю провідника.
Індуктивність \(L\) - це фізична величина, що характеризує провідник і чисельно дорівнює ЕРС самоіндукції, яка виникає в провіднику при зміні сили струму на 1 ампер за 1 секунду:
В Міжнародній системі одиниць (СІ) індуктивність вимірюється в генрі (Гн, H). Ця одиниця названа на честь американського фізика Джозефа Генрі (1797–1878), який відкрив явище самоіндукції у 1831 році.
За визначенням, індуктивність провідника становить 1 генрі, якщо в ньому виникає ЕРС самоіндукції 1 вольт при зміні сили струму на 1 ампер за 1 секунду:
Обмотки генераторів і електродвигунів характеризуються значною індуктивністю. При розмиканні кола, коли сила струму змінюється швидко, ЕРС самоіндукції може досягти таких значень, що призведе до пробою ізоляції.
Індуктивність - це характеристика провідника, тому вона не залежить ані від сили струму в провіднику, ані від ЕРС самоіндукції, що виникає в провіднику внаслідок зміни струму. Індуктивність залежить:
від магнітних властивостей середовища, в якому розташований провідник;
розмірів і форми провідника (індуктивність прямого проводу набагато менша, ніж індуктивність того самого проводу, намотаного на олівець);
наявності та форми осердя.
Наприклад, індуктивність соленоїда обчислюють за формулою:
де \(\mu\) - відносна магнітна проникність матеріалу, з якого виготовлено осердя (магнітну проникність матеріалу будемо вивчати далі по нашому курсу); \(\mu_0\) - магнітна стала; \(N\) - кількість витків у соленоїді; \(l\) і \(S\) - довжина і площа поперечного перерізу соленоїда відповідно.
Як обчислити енергію магнітного поля#
Розглянемо, яким чином вихрове електричне поле підтримує струм у колі після вимкнення джерела живлення. Логічно припустити, що енергія накопичується у магнітному полі провідника (котушки) ще до моменту розмикання кола. Аналізуючи процес, можемо зробити такі спостереження:
Джерело живлення починає працювати одразу після замикання кола, проте струм досягає максимального значення не миттєво. Це свідчить про те, що протягом проміжку часу від нуля 0 до моменту часу \(t_1\) (коли досягається максимальне значення сили струму) енергія джерела витрачається не лише на рух зарядів.
Протягом цього ж проміжку часу (від 0 до \(t_1\)) навколо котушки формується помітне магнітне поле, і жодних інших змін не спостерігається. Отже, енергія витрачається саме на формування магнітного поля.
Закономірно, що чим більшого значення досягає сила струму в котушці, тим більше енергії накопичується. Крім того, енергія магнітного поля зростає зі збільшенням індуктивності \(L\) котушки, оскільки в цьому випадку струм повільніше досягає максимального значення.
На основі математичних розрахунків з використанням інтегрування (ці розрахунки поки що опускаємо) отримуємо формулу для визначення енергії магнітного поля:
Таким чином, енергія магнітного поля провідника зі струмом дорівнює половині добутку індуктивності провідника на квадрат сили струму в провіднику.
Індуктивність подібна до маси в механіці:
Щоб зрушити тіло (надати йому швидкості), потрібно виконати роботу: \(A = E_k = \frac{mv^2}{2}\); чим більша маса тіла, тим більшу роботу треба виконати; під час гальмування тіло саме виконує роботу.
Аналогічно для створення струму потрібно виконати роботу проти сил вихрового поля: \(A = W = \frac{LI^2}{2}\); чим більша індуктивність провідника, тим більшу роботу треба виконати; під час зменшення струму вихрове електричне поле саме виконує роботу.
Приклад задачі#
Задача. Надпровідну котушку з індуктивністю 10.0 Гн підключають до джерела струму з ЕРС 50 В і незначним внутрішнім опором. Вважаючи, що сила струму в котушці зростає рівномірно, визначте час, за який сила струму досягне 10 А.
Дано:
\(R = 0\)
\(L = 10.0\) Гн
\(I_0 = 0\)
\(\varepsilon_{дж} = 50\) В
\(r = 0\)
\(I = 10\) А
Знайти: \(t\)
Розв'язання: Сила струму в котушці зростає поступово внаслідок явища самоіндукції. Для розв'язання задачі застосуємо закон Ома для повного кола:
У цьому випадку повна ЕРС кола \(\varepsilon\) складається з ЕРС джерела та ЕРС самоіндукції:
\(\varepsilon = \varepsilon_{дж} + \varepsilon_{is}\)
де \(\varepsilon_{is} = -L\frac{\Delta I}{\Delta t}\).
Отже, маємо:
Оскільки \((R+r) = 0\), то \(\varepsilon_{дж} = L\frac{\Delta I}{\Delta t}\), звідки
де \(\frac{\Delta I}{\Delta t}\) - швидкість зміни сили струму.
Враховуючи, що струм у котушці змінюється рівномірно, час, за який він досягне значення 10 А, обчислюємо за формулою:
Перевіримо одиницю вимірювання:
Обчислимо числове значення:
Відповідь: \(t = 2\) с.

